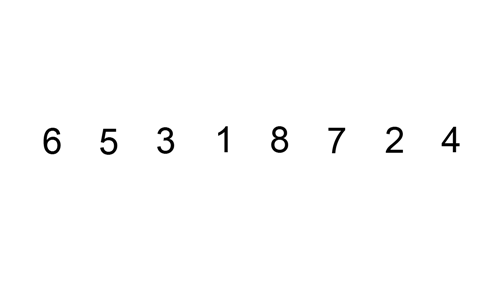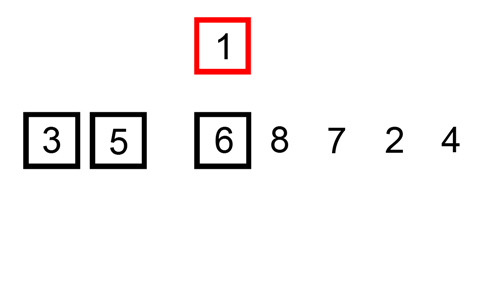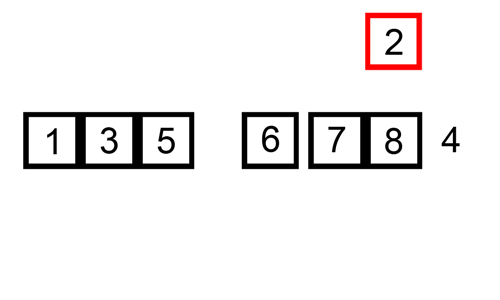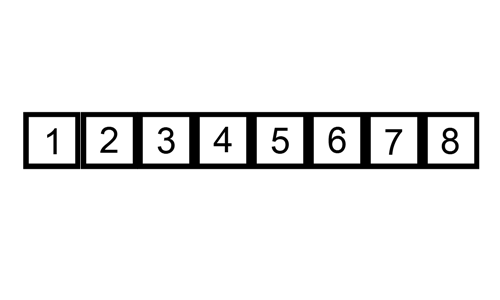Chapter 23: Algorithms

Linear search

Linear search: Start at the first element of the array and check each element in turn until the search value is found or the end of the array is reached.

Bubble sort

Sorting elements in a 1D array

The simplest way to sort an unordered list of values is the following method.

Compare the first and second values. If the first value is larger than the second value, swap them.
Compare the second and third values. If the second value is larger than the third value, swap them.
Compare the third and fourth values. If the third value is larger than the fourth value, swap them.
Keep on comparing adjacent values, swapping them if necessary, until the last two values in the list have been processed.

In effect we perform a loop within a loop, a nested loop. This method is known as a bubble sort. The name comes from the fact that smaller values slowly rise to the top, like bubbles in a liquid.

Identifier	Data type	Explanation
MyList	ARRAY[1:n] OF INTEGER	Data structure (1D array) to store seven numbers
NoSwaps	BOOLEAN	Whether swap items in the loop
n	INTEGER	The upper bound of the array
j	INTEGER	Counter for inner loop
Temp	INTEGER	Variable for temporary storage while swapping values

Pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


# index starts from 1
REPEAT
    NoSwaps ← TRUE
    FOR j ← 1 TO n
        IF MyList[j] > MyList[j + 1]
            THEN
                Temp ← MyList[j]
                MyList[j] ← MyList[j + 1]
                MyList[j + 1] ← Temp
                NoSwaps ← FALSE
        ENDIF
    ENDFOR
    n ← n - 1
UNTIL NoSwaps ← TRUE

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def bubble(unsorted):
    noswap = False
    length = len(unsorted)-1
    while noswap == False:
        noswap = True
        for i in range(length):
            if unsorted[i] > unsorted[i+1]:
                unsorted[i],unsorted[i+1] = unsorted[i+1],unsorted[i]
                noswap = False
        length = length - 1
    return unsorted

Insertion sort

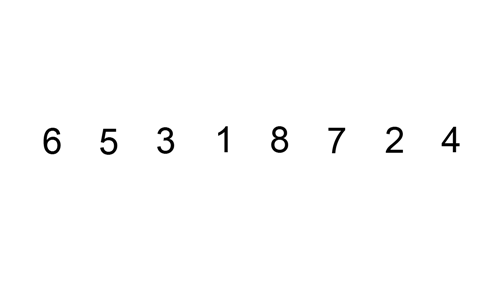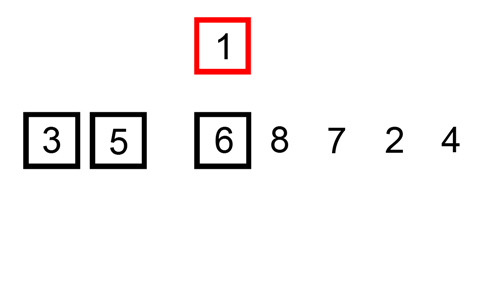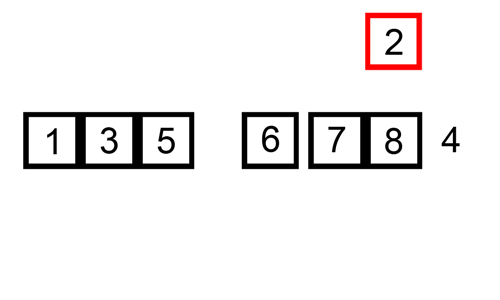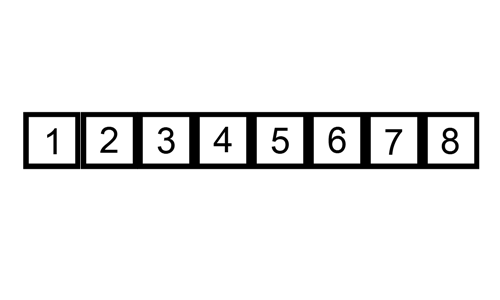
Click img to check the source page(pediaa.com)

Repeat the following steps until all cards in the unsorted pile have been inserted into the correct position.

Repeat until the card to be inserted has been placed in its correct position.
Compare the current card with the card to be inserted.
If the card to be inserted is greater than the current card, insert it below the current card.
Otherwise, if there is a card above the current card in your hand, make this your new current card.
If there is no new current card, place the card to be inserted at the top of the sorted pile.

Pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


# index starts from 1
# TOTAL : N
FOR i ← 2 TO N
    Temp ← Number [ i ]
    j ← i – 1
    WHILE ( Number [ j ] > Temp ) AND ( j > 0 )
        Number [ j + 1 ] ← Number [ j ]
        j ← j - 1
    ENDWHILE
    Number [ j + 1 ] ← Temp
ENDFOR

Python

1
2
3
4
5
6
7
8


def insertion(unsorted):
    for i in range(1,len(unsorted)):
        j = i - 1
        if unsorted[i] < unsorted[j]:
            while j>=0 and unsorted[i] < unsorted[j]:
                unsorted[i],unsorted[j] = unsorted[j],unsorted[i]
                j,i = j-1,i-1
    return unsorted

Difference between Bubble sort & Insertion sort

Click img to check the source page(pediaa.com)

Binary search

Binary search: repeated checking of the middle item in an ordered search list and discarding the half of the list which does not contain the search item.

Pseudocode

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


# index starts from 1
Found ← FALSE
SearchFailed ← FALSE
First ← 1
Last ← Total
WHILE ( NOT Found ) AND ( NOT SearchFailed )
    Middle ← ( First + Last ) / 2
    IF Number [ Middle ] = SearchNumber
        THEN
            Found ← TRUE
        ELSE
            IF First >= Last
                THEN
                    SearchFailed ← TRUE
                ELSE
                    IF Number [ Middle ] > SearchNumber
                        THEN
                            Last ← Middle - 1
                        ELSE
                            First ← Middle+ 1
                    ENDIF
            ENDIF
	ENDIF
ENDWHILE
IF Found = TRUE
    THEN
        OUTPUT Middle
    ELSE
        OUTPUT " Number is not found "
ENDIF

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def binary_search(alist,item):
    found = False
    first = 0
    last = len(alist)
    while found == False and first < last:
        key = (first+last)//2
        if item == alist[key]:
            found = True
        elif item < alist[key]:
            last = key - 1
        else:
            first = key + 1
    return found

Abstract Data Types (ADTs)

Linked lists

Pseudocode

Create a new linked list

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// NullPointer should be set to -1 if using array element with index 0
CONSTANT NullPointer = –1
// Declare record type to store data and pointer
TYPE ListNode
    DECLARE Data : STRING
    DECLARE Pointer : INTEGER
ENDTYPE
DECLARE StartPointer : INTEGER
DECLARE FreeListPtr : INTEGER
DECLARE List : ARRAY[0 : n] OF ListNode
PROCEDURE InitialiseList
    StartPointer ← NullPointer // set start pointer
    FreeListPtr ← 0 // set starting position of free list
    FOR Index ← 0 TO n-1 // link all nodes to make free list
        List[Index].Pointer ← Index + 1
    NEXT Index
    List[n].Pointer ← NullPointer // last node of free list
ENDPROCEDURE

Insert a new node into an ordered linked list

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


PROCEDURE InsertNode(NewItem)
    IF FreeListPtr <> NullPointer
        THEN // there is space in the array
            // take node from free list and store data item
            NewNodePtr ← FreeListPtr
            List[NewNodePtr].Data ← NewItem
            FreeListPtr ← List[FreeListPtr].Pointer
            // find insertion point
            ThisNodePtr ← StartPointer // start at beginning of list
            PreviousNodePtr ← NullPointer
            WHILE ThisNodePtr <> NullPointer // while not end of list
                AND List[ThisNodePtr].Data < NewItem DO
                    PreviousNodePtr ← ThisNodePtr // remember this node
                    // follow the pointer to the next node
                    ThisNodePtr ← List[ThisNodePtr].Pointer
            ENDWHILE
            IF PreviousNodePtr = StartPointer
                THEN // insert new node at start of list
                    List[NewNodePtr].Pointer ← StartPointer
                    StartPointer ← NewNodePtr
                ELSE // insert new node between previous node and this node
                    List[NewNodePtr].Pointer ← List[PreviousNodePtr].Pointer
                    List[PreviousNodePtr].Pointer ← NewNodePtr
            ENDIF
    ENDIF
ENDPROCEDURE

Find an element in an ordered linked list

1
2
3
4
5
6
7
8
9


FUNCTION FindNode(DataItem) RETURNS INTEGER // returns pointer to node
    CurrentNodePtr ← StartPointer // start at beginning of list
    WHILE CurrentNodePtr <> NullPointer // not end of list
        AND List[CurrentNodePtr].Data <> DataItem DO // item not found
            // follow the pointer to the next node
            CurrentNodePtr ← List[CurrentNodePtr].Pointer
    ENDWHILE
    RETURN CurrentNodePtr // returns NullPointer if item not found
ENDFUNCTION

Delete a node from an ordered linked list

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


PROCEDURE DeleteNode(DataItem)
    ThisNodePtr ← StartPointer
    WHILE ThisNodePtr <> NullPointer
        AND List[ThisNodePtr].Data <> DataItem DO
            PreviousNodePtr ← ThisNodePtr
            ThisNodePtr ← List[ThisNodePtr].Pointer
    ENDWHILE
    IF ThisNodePtr <> NullPointer
        THEN
            IF ThisNodePtr = StartPointer
                THEN
                    StartPointer ← List[StartPointer].Pointer
                ELSE
                    // it is not the start node;
                    // so make the previous node’s pointer point to
                    // the current node’s 'next' pointer; thereby removing all
                    // references to the current pointer from the list
                    List[PreviousNodePtr].Pointer ← List[ThisNodePtr].Pointer
            ENDIF
            List[ThisNodePtr].Pointer ← FreeListPtr
            FreeListPtr ← ThisNodePtr
    ENDIF
ENDPROCEDURE

Access all nodes stored in the linked list

1
2
3
4
5
6
7
8


PROCEDURE OutputAllNodes
    CurrentNodePtr ← StartPointer // start at beginning of list
    WHILE CurrentNodePtr <> NullPointer DO // while not end of list
        OUTPUT List[CurrentNodePtr].Data
        // follow the pointer to the next node
        CurrentNodePtr ← List[CurrentNodePtr].Pointer
    ENDWHILE
ENDPROCEDURE

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55


#Python program for finding an item in a linked list
myLinkedList = [27, 19, 36, 42, 16, None, None, None, None, None, None, None]
myLinkedListPointers = [-1, 0, 1, 2, 3 ,6 ,7 ,8 ,9 ,10 ,11, -1]
startPointer = 4
nullPointer = -1
def find(itemSearch):
    found = False
    itemPointer = startPointer
    while itemPointer != nullPointer and not found:
        if myLinkedList[itemPointer] == itemSearch:
            found = True
        else:
            itemPointer = myLinkedListPointers[itemPointer]
    return itemPointer
#enter item to search for
item = int(input("Please enter item to be found "))
result = find(item)
if result != -1:
    print("Item found")
else:
    print("Item not found")


#Python program for adding an item in a linked list
def insert(itemAdd):
    global startPointer
    if heapStartPointer == nullPointer:
        print("Linked List full")
    else:
        tempPointer = startPointer
        startPointer = heapStartPointer
        heapStartPointer = myLinkedListPointers[heapStartPointer]
        myLinkedList[startPointer] = itemAdd
        myLinkedListPointers[startPointer] = tempPointer



#The following procedure deletes an item from a linked list.
def delete(itemDelete):
    global startPointer, heapStartPointer
    if startPointer == nullPointer:
        print("Linked List empty")
    else:
        index = startPointer
        while myLinkedList[index] != itemDelete and index != nullPointer:
            oldindex = index
            index = myLinkedListPointers[index]
    if index == nullPointer:
        print("Item ", itemDelete, " not found")
    else:
        myLinkedList[index] = None
        tempPointer = myLinkedListPointers[index]
        myLinkedListPointers[index] = heapStartPointer
        heapStartPointer = index
        myLinkedListPointers[oldindex] = tempPointer

Binary trees

Write algorithms to find an item in each of the following: linked list, binary tree
Write algorithms to insert an item into each of the following: stack, queue, linked list, binary tree
Write algorithms to delete an item from each of the following: stack, queue, linked list
Show understanding that a graph is an example of an ADT.
Describe the key features of a graph and justify its use for a given situation
If the data value is greater than the current node’s data value, follow the right branch.
If the data value is smaller than the current node’s data value, follow the left branch.

We can store the binary tree in an array of records (see Figure 23.05). One record represents a node and consists of the data and a left pointer and a right pointer. Unused nodes are linked together to form a free list.

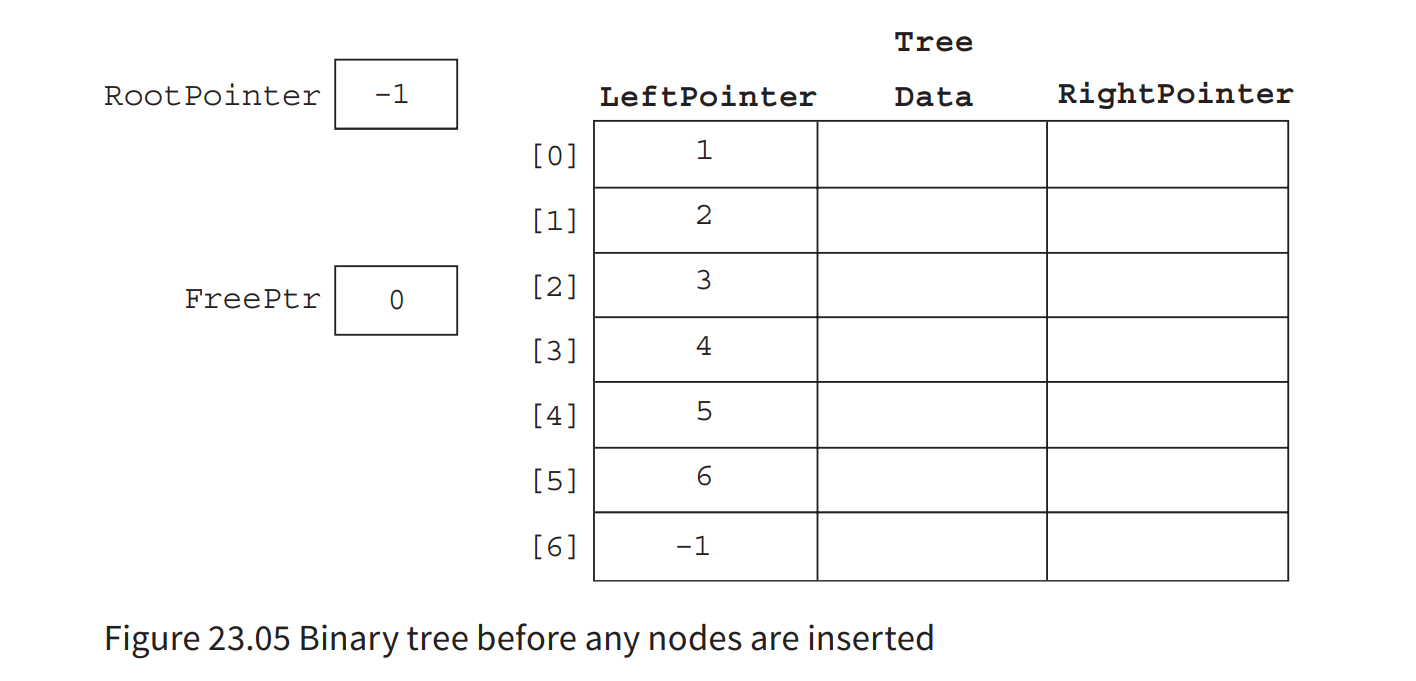
Pseudocode

Create a new binary tree

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


// NullPointer should be set to -1 if using array element with index 0
CONSTANT NullPointer = –1
// Declare record type to store data and pointers
TYPE TreeNode
    DECLARE Data : STRING
    DECLARE LeftPointer : INTEGER
    DECLARE RightPointer : INTEGER
ENDTYPE
DECLARE RootPointer : INTEGER
DECLARE FreePtr : INTEGER
DECLARE Tree : ARRAY[0 : 6] OF TreeNode

PROCEDURE InitialiseTree
    RootPointer ← NullPointer // set start pointer
    FreePtr ← 0 // set starting position of free list
    FOR Index ← 0 TO 5 // link all nodes to make free list
        Tree[Index].LeftPointer ← Index + 1
    NEXT Index
    Tree[6].LeftPointer ← NullPointer // last node of free list
ENDPROCEDURE

Insert a new node into a binary tree

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


PROCEDURE InsertNode(NewItem)
    IF FreePtr <> NullPointer
        THEN // there is space in the array
             // take node from free list, store data item, set null pointers
        NewNodePtr ← FreePtr
        FreePtr ← Tree[FreePtr].LeftPointer
        Tree[NewNodePtr].Data ← NewItem
        Tree[NewNodePtr].LeftPointer ← NullPointer
        Tree[NewNodePtr].RightPointer ← NullPointer

    // check if empty tree
        IF RootPointer = NullPointer
            THEN // insert new node at root
                RootPointer ← NewNodePtr
            ELSE // find insertion point
                ThisNodePtr ← RootPointer // start at the root of the tree
                WHILE ThisNodePtr <> NullPointer DO     // while not a leaf node
                    PreviousNodePtr ← ThisNodePtr       // remember this node
                    IF Tree[ThisNodePtr].Data > NewItem
                        THEN // follow left pointer
                            TurnedLeft ← TRUE
                            ThisNodePtr ← Tree[ThisNodePtr].LeftPointer
                        ELSE // follow right pointer
                            TurnedLeft ← FALSE
                            ThisNodePtr ← Tree[ThisNodePtr].RightPointer
                    ENDIF
                ENDWHILE
                IF TurnedLeft = TRUE
                    THEN
                        Tree[PreviousNodePtr].LeftPointer ← NewNodePtr
                ELSE
                        Tree[PreviousNodePtr].RightPointer ← NewNodePtr
                ENDIF
        ENDIF
    ENDIF
ENDPROCEDURE

Find a node in a binary tree

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


FUNCTION FindNode(SearchItem) RETURNS INTEGER // returns pointer to node
    ThisNodePtr ← RootPointer // start at the root of the tree
    WHILE ThisNodePtr <> NullPointer // while a pointer to follow
        AND Tree[ThisNodePtr].Data <> SearchItem DO // and search item not found
            IF Tree[ThisNodePtr].Data > SearchItem
                THEN // follow left pointer
                    ThisNodePtr ← Tree[ThisNodePtr].LeftPointer
                ELSE // follow right pointer
                    ThisNodePtr ← Tree[ThisNodePtr].RightPointer
            ENDIF
    ENDWHILE
    RETURN ThisNodePtr // will return null pointer if search item not found
ENDFUNCTION

Python

1
2
3
4
5
6
7
8
9


def FindLeaves(CurrentNode): 
    global BinaryTree 
    if(BinaryTree[CurrentNode].LeftPointer != -1): 
        FindLeaves(BinaryTree[CurrentNode].LeftPointer) 
    if(BinaryTree[CurrentNode].RightPointer != -1): 
        FindLeaves(BinaryTree[CurrentNode].RightPointer) 
    if((BinaryTree[CurrentNode].RightPointer == -1) and (BinaryTree[CurrentNode].LeftPointer == -1)): 
        print BinaryTree[CurrentNode].DataValue
    return 

Stacks

Note that BaseOfStackPointer will always point to element 0 of the array.
TopOfStackPointer will vary. It will increase when an item is pushed- onto the stack and it will decrease when an item is popped off the stack.
When the stack is empty, TopOfStackPointer will have the value –1.

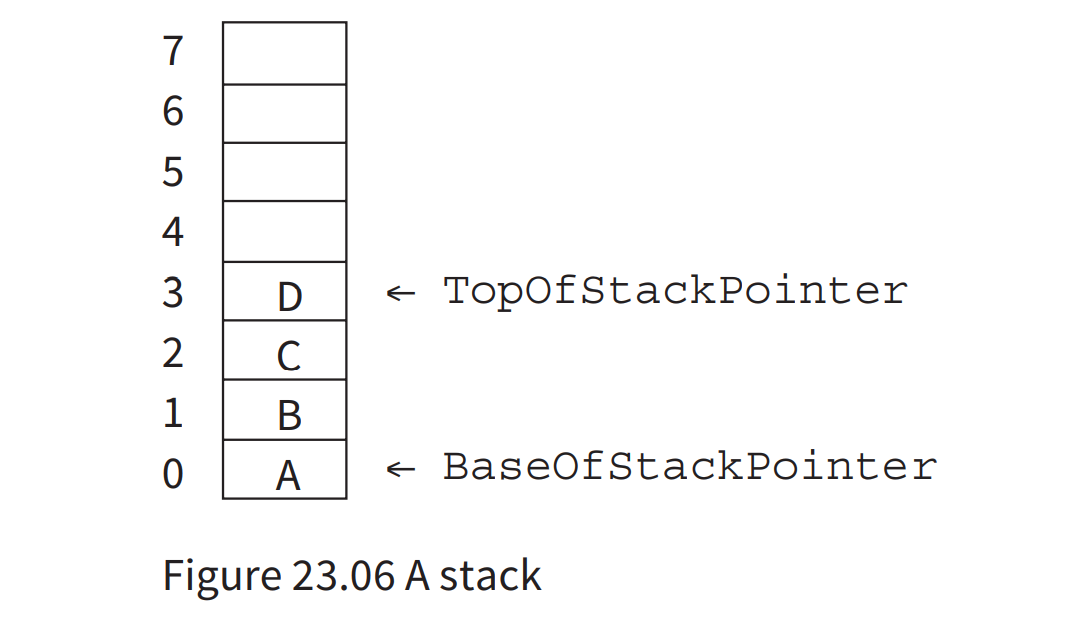
Pseudocode

Create a new stack

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


CONSTANT EMPTYSTRING = ""
CONSTANT NullPointer = –1
CONSTANT MaxStackSize = n
DECLARE BaseOfStackPointer : INTEGER
DECLARE TopOfStackPointer : INTEGER
DECLARE Stack : ARRAY[0 : MaxStackSize – 1] OF STRING
PROCEDURE InitialiseStack
    BaseOfStackPointer ← 0 // set base of stack pointer
    TopOfStackPointer ← NullPointer // set top of stack pointer
ENDPROCEDURE

Push an item onto the stack

1
2
3
4
5
6
7
8
9


PROCEDURE Push(NewItem)
    IF TopOfStackPointer < MaxStackSize – 1
        THEN   // there is space on the stack
               // increment top of stack pointer
            TopOfStackPointer ← TopOfStackPointer + 1
               // add item to top of stack
            Stack[TopOfStackPointer] ← NewItem
    ENDIF
ENDPROCEDURE

Pop an item off the stack

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


FUNCTION Pop()
    DECLARE Item : STRING
    Item ← EMPTYSTRING
    IF TopOfStackPointer > NullPointer
        THEN // there is at least one item on the stack
             // pop item off the top of the stack
            Item ← Stack[TopOfStackPointer]
            Stack[TopOfStackPointer] ← EMPTYSTRING
             // decrement top of stack pointer
            TopOfStackPointer ← TopOfStackPointer – 1
    ENDIF
    RETURN Item
ENDFUNCTION

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


def init_stack(n):
    base_pointer = 0
    top_pointer = -1
    stack = ["" for i in range(n)]

def add_item(item):
    global base_pointer
    global top_pointer
    global stack
    if top_pointer+1 == len(stack):
        return "stack is full"
    else:
        stack[top_pointer+1]=item
        top_pointer = top_pointer+1
        return "success"

def pop_item():
    global base_pointer
    global top_pointer
    global stack
    if top_pointer == -1:
        return "stack is empty"
    else:
        stack[top_pointer] = ""
        top_pointer = top_pointer-1
        return "success"

Queues

FrontOfQueuePointer always points to the first element in the queue, that is the next element to be taken from the queue. EndOfQueuePointer always points to the last element in the queue. Before another element joins the queue, the EndOfQueuePointer is incremented.

To make it easier to test whether the queue is empty or full, a counter variable can be used.

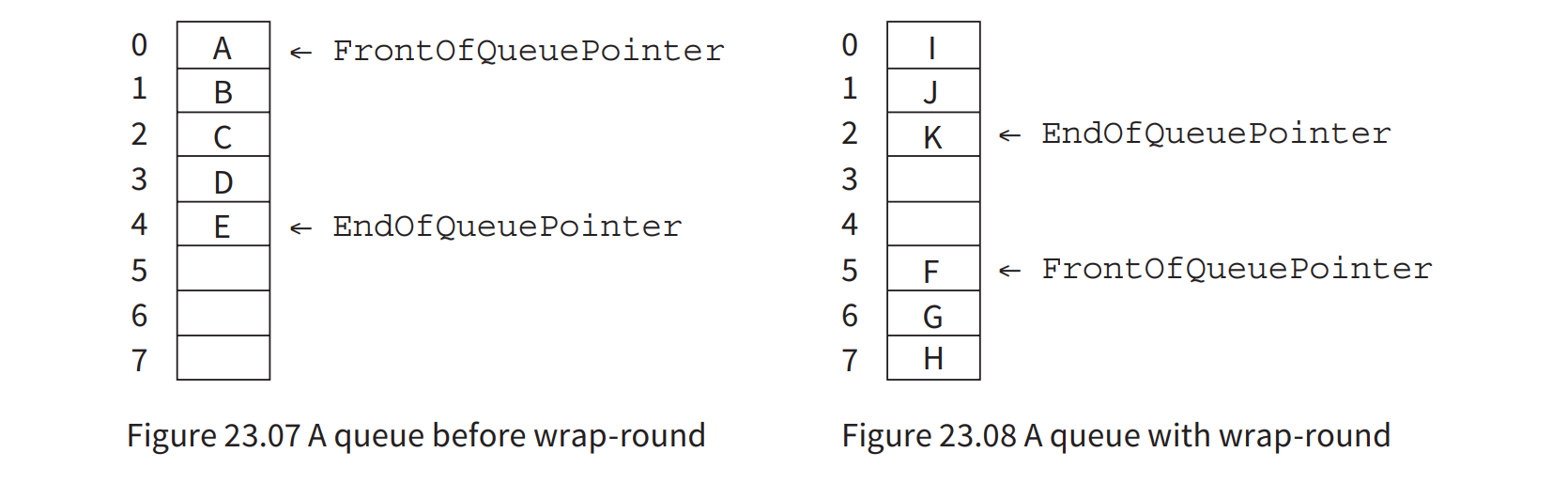
Pseudocode

Create a new queue

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


CONSTANT EMPTYSTRING = ""
CONSTANT NullPointer = -1
CONSTANT MaxQueueSize = 8
DECLARE FrontOfQueuePointer : INTEGER
DECLARE EndOfQueuePointer : INTEGER
DECLARE NumberInQueue : INTEGER
DECLARE Queue : ARRAY[0 : MaxQueueSize – 1] OF STRING
PROCEDURE InitialiseQueue
    FrontOfQueuePointer ← NullPointer // set front of queue pointer
    EndOfQueuePointer ← NullPointer   // set end of queue pointer
    NumberInQueue ← 0                 // no elements in queue
ENDPROCEDURE

Add an item to the queue

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


PROCEDURE AddToQueue(NewItem)
    IF NumberInQueue < MaxQueueSize
        THEN // there is space in the queue
             // increment end of queue pointer
            EndOfQueuePointer ← EndOfQueuePointer + 1
             // check for wrap-round
            IF EndOfQueuePointer > MaxQueueSize – 1
                THEN // wrap to beginning of array
                    EndOfQueuePointer ← 0
                     // add item to end of queue
            ENDIF
            Queue[EndOfQueuePointer] ← NewItem
            // increment counter
            NumberInQueue ← NumberInQueue + 1
    ENDIF
ENDPROCEDURE

Remove an item from the queue

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


FUNCTION RemoveFromQueue()
    DECLARE Item : STRING
    Item ← EMPTYSTRING
    IF NumberInQueue > 0
        THEN // there is at least one item in the queue
             // remove item from the front of the queue
            Item ← Queue[FrontOfQueuePointer]
            NumberInQueue ← NumberInQueue – 1
            IF NumberInQueue = 0
                THEN // if queue empty, reset pointers
                    CALL InitialiseQueue
                ELSE
                    // increment front of queue pointer
                    FrontOfQueuePointer ← FrontOfQueuePointer + 1
                    // check for wrap-round
                    IF FrontOfQueuePointer > MaxQueueSize – 1
                        THEN // wrap to beginning of array
                            FrontOfQueuePointer ← 0
                    ENDIF
            ENDIF
    ENDIF
    RETURN Item
ENDFUNCTION

Python

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30


def init_queue(n):
    queue = ["" for i in range(n)]
    frontpointer = 0
    endpointer = 0

def add_item(item):
    global queue
    global frontpointer
    global endpointer
    if "" in queue == False:
        return "queue is full"
    else:
        if endpointer+1 == len(queue):
            queue[0] = item
            endpointer = 0
        else:
            queue[endpointer+1]=item
            endpointer = endpointer+1
        return "success"

def pop_item():
    global queue
    global frontpointer
    global endpointer
    if frontpointer+1 == len(queue):
        queue[frontpointer] = ""
        frontpointer = 0
    else:
        queue[frontpointer] = ""
        frontpointer = frontpointer + 1

Graphs

Graphs are used to record relationships between things.
A labelled (weighted) graph has edges with values representing something.
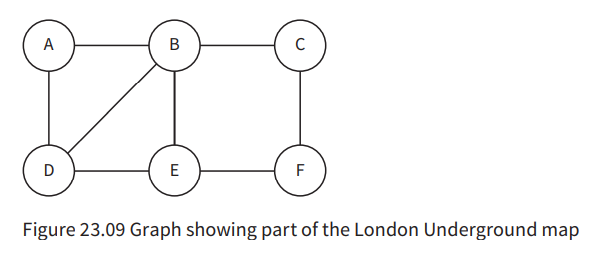
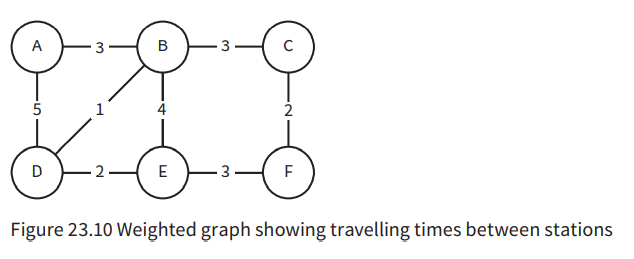
Graphs can be directed or undirected. 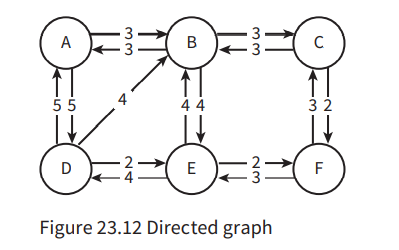To implement a graph, we can use an adjacency matrix or an adjacency list. An adjacency matrix stores the relationship between every vertex to all other vertices.
For an unweighted graph, a 1 represents an edge, a 0 no edge. When weights are to be recorded, the weight replaces the 1. Instead of a 0, we use the infinity symbol ∞.
For a weighted graph, the connection as well as the weight is stored in the list.

Hash tables

To store records in an array and have direct access to records, we can use the concept of a hash table.
We calculate an address (the array index) from the key value of the record and store the record at this address. When we search for a record, we calculate the address from the key and go to the calculated address to find the record. Calculating an address from a key is called ‘hashing’.

Finding a hashing function that will give a unique address from a unique key value is very difficult. If two different key values hash to the same address this is called a ‘collision’. There are different ways to handle collisions:

chaining: create a linked list for collisions with start pointer at the hashed address
using overflow areas: all collisions are stored in a separate overflow area, known as ‘closed hashing’
using neighbouring slots: perform a linear search from the hashed address to find an empty slot, known as ‘open hashing’

Pseudocode

Insert a record into a hash table

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


PROCEDURE Insert(NewRecord)
    Index ← Hash(NewRecord.Key)
    WHILE HashTable[Index] NOT empty DO
        Index ← Index + 1 // go to next slot to check if empty
        IF Index > Max    // beyond table boundary?
            THEN          // wrap around to beginning of table
                Index ← 0
        ENDIF
    ENDWHILE
    HashTable[Index] ← NewRecord
ENDPROCEDURE

Find a record in a hash table

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


FUNCTION FindRecord(SearchKey) RETURNS Record
    Index ← Hash(SearchKey)
    WHILE (HashTable[Index].Key <> SearchKey) AND (HashTable[Index] NOT empty) DO
        Index ← Index + 1     // go to next slot
        IF Index > Max        // beyond table boundary?
            THEN              // wrap around to beginning of table
                Index ← 0
        ENDIF
    ENDWHILE
    IF HashTable[Index] NOT empty   // if record found
        THEN
            RETURN HashTable[Index] // return the record
    ENDIF
ENDFUNCTION

Dictionaries

An ADT dictionary in computer science is implemented using a hash table (see Section 23.11), so that a value can be looked up using a direct-access method.

Pseudocode

1
2
3
4
5
6


TYPE DictionaryEntry
    DECLARE Key : STRING
    DECLARE Value : STRING
ENDTYPE
DECLARE EnglishFrench : ARRAY[0 : 999] OF DictionaryEntry // empty dictionary
ENDTYPE

Big O notation

A way of comparing the eff iciency of algorithms has been devised using order of growth as a function of the size of the input.
Big O notation is used to classify algorithms according to how their running time (or space requirements) grows as the input size grows.

Order of growth (time complexity) for data input set of size n

Order of growth	Example	Explanation
$O(1)$	FUNCTION GetFirstItem(List : ARRAY) RETURN List[1]	The complexity of the algorithm does not change regardless of data set size
$O(n)$	Linear search Bubble sort performed on an already sorted list	Linear growth
$O(Log_2 n)$	Binary search	The total time taken increases as the data set size increases, but each comparison halves the data set. So the time taken increases by smaller amounts and approaches constant time.
$O(n^2)$	Bubble sort Insertion sort	Polynomial growth Common with algorithms that involve nested iterations over the data set
$O(n^3)$		Polynomial growth Deeper nested iterations will result in $O(n^3)$ , $O(n^4)$ , …
$O(2^n)$	Recursive calculation of Fibonacci numbers	Exponential growth

Space complexity refers to the amount of memory required for a growing number of values n in the dataset.

The ADT operations discussed in this chapter have space complexity O(n). This means that they only take the space required for the data set. Bubble sort and insertion sort have space complexity of O(1). This means they do not require extra memory for sorting larger lists.